曲面を表す2変数関数 \(z = f(x, y)\) に対して \[ \begin{eqnarray} dz &=&f_{x}dx + f_{y}dy\\ &=& \frac{ \partial f }{ \partial x }dx + \frac{ \partial f }{ \partial y }dy \end{eqnarray} \] を全微分といいますね。
これを初めてみたとき、この式の形で微分といっていいのか?と思った人もいると思いますが、この式で問題ありません。なぜなら、これは\(xとy\)の2つの変数の変化量に対する\(z\)の変化量を表すからです。微分が変化量の極限であったことを考えればこれも微分です。
さて、一度偏微分の定義に戻ってみましょう。それぞれの導関数は次の通りです。 \[ \begin{cases} \displaystyle \frac{ \partial f }{ \partial x } = f_{x}(x, y) = \displaystyle \lim_{ h \to 0 } \frac{ f(x + h, y) – f(x, y) }{ h }\\ \displaystyle \frac{ \partial f }{ \partial y } = f_{y}(x, y) = \displaystyle \lim_{ k \to 0 } \frac{ f(x, y + k) – f(x, y) }{ k } \end{cases} \]
これを見るとわかる通り、
\( \begin{cases} xの偏導関数 \frac{ \partial f }{ \partial x } を求めるときはyが定数\\ yの偏導関数 \frac{ \partial f }{ \partial y } を求めるときはxが定数 \end{cases} \)
つまり、
\( \begin{cases} xの変化だけによるzの変化が \frac{ \partial f }{ \partial x }\\ yの変化だけによるzの変化が \frac{ \partial f }{ \partial y } \end{cases} \)
というわけです。
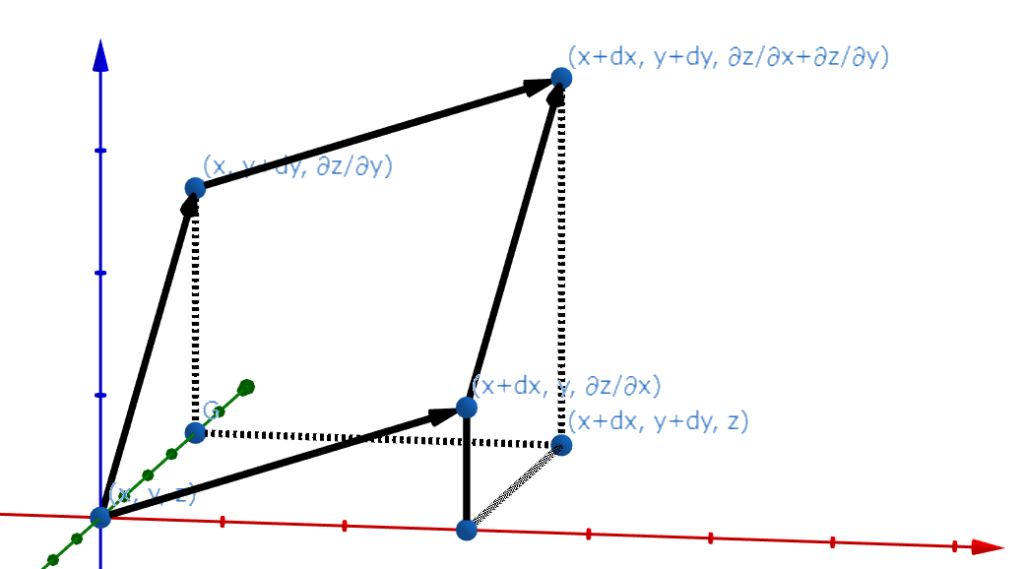
次の図は、線形結合っぽいことを伝えようと思った図です。
原点が\((x, y, z)\)です。 よくわからないごみ画像になってしまいましたが、\(xとy\)の偏微分の関係が伝わってくれればうれしいです。
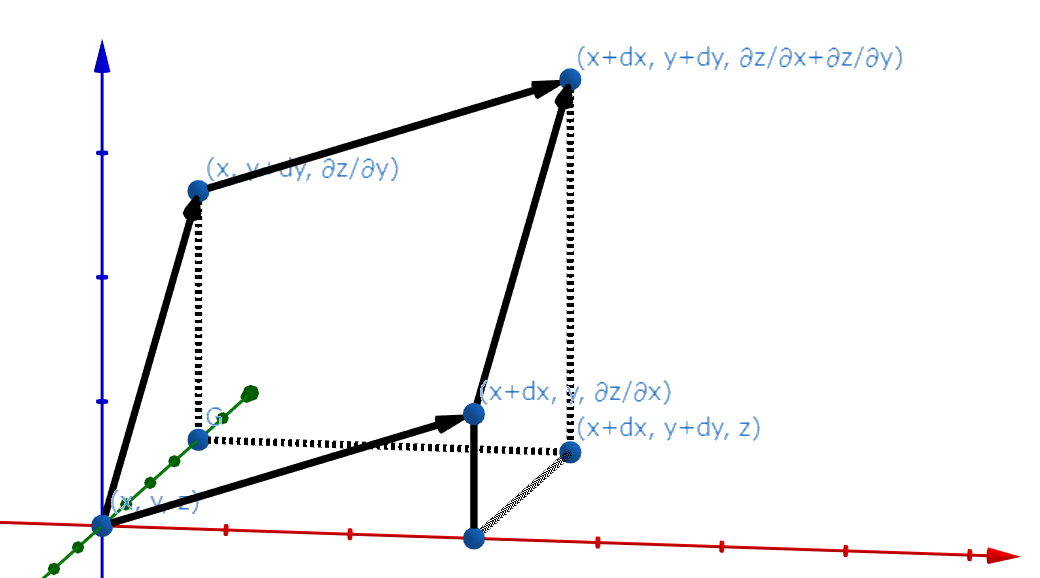
とにかく、\(x\)による変化と\(y\)による変化があり、これらは独立な成分なので足すことで\(xとy\)による\(z\)の変化がわかるということです。
また、全微分の理解と同時に接平面の方程式も線形結合で理解できます。
曲面\(z=f(x, y)\)上の点\((a, b, c)\)における接平面の方程式は\[z – c = f_{x}(a, b)(x – a) + f_{y}(a, b)(y – b)\]です。
私の雑な解釈ですが、全微分の式において \[ \begin{cases} dx:\Delta x = x – a\\ dy:\Delta y = y – b\\ dz:\Delta z = z – c \end{cases}\] とすれば、この方程式を満たす点の集まりは接平面になることがわかります。