注意
この記事は、平行移動の公式に納得していない人や、私のような数学のすの字も忘れた人や平行移動ってどうやるんだっけというくらいすべてを忘れた方向けです。\(y = x^2\)を平行移動
さっそくですが \(y = x^2\) を \(\begin{cases} x方向に +2 \\ y方向に +3 \end{cases}\) だけ平行移動させたグラフになる関数を求められますか?
答えは、\(y – 3 = (x – 2)^2 (y = (x – 2)^2+3)\) ですよね。
こうなる理由を今回は説明します。
実は写像で考えると簡単なことです
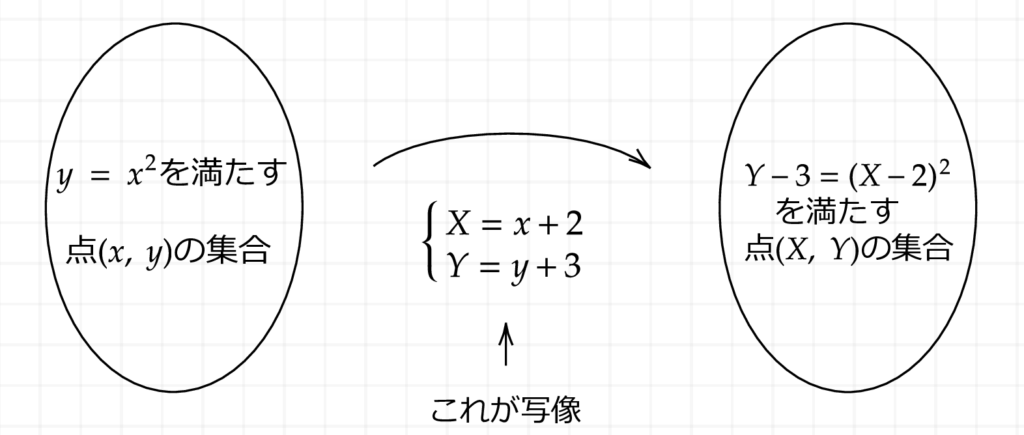
まず、平行移動後の関数を満たす座標\((X, Y)\)の集合を考えましょう。このとき、\(y = x^2\)を満たす\((x, y)\)を用いると、\[\begin{cases} X = x + 2 \\ Y = y + 3 \end{cases}\]という関係があることがわかりますね。
\((x, y)\)は\(y = x^2\)を満たすので、\(xとy\)を消去(代入)して\(XとY\)の関係式にすると、\[Y – 3 = (X – 2)^2\]となり、この関数が平行移動後のグラフを表しますね。
あるいは、 \(\begin{cases} x = t \\ y = t^2 \end{cases}\) だから \(\begin{cases} X = t + 2 \\ Y = t^2 + 3 \end{cases}\) としてパラメータ\(t\)を消してもOKです。
おまけ
平行移動であることを考えると当然かもしれませんが、
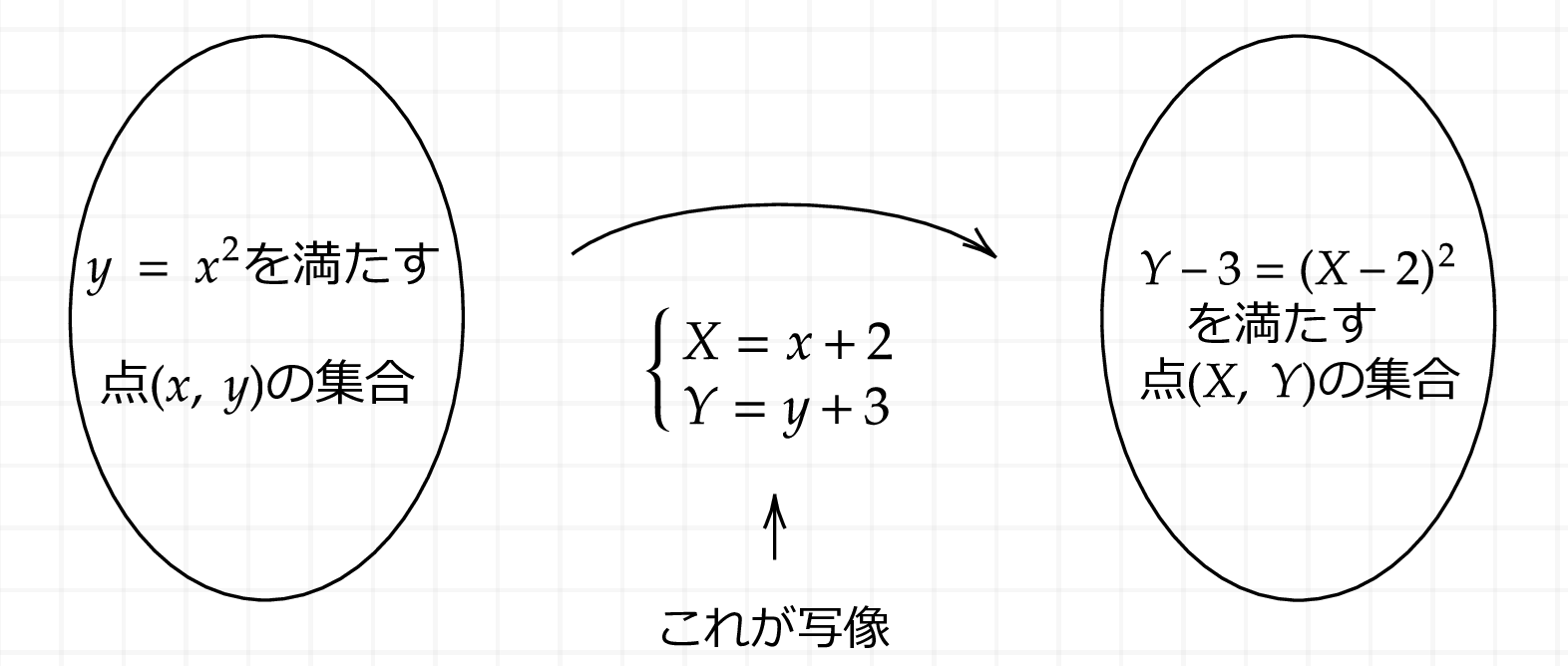
これが写像であり、全単射であることを簡単に確認しておきましょう。1.\((x, y)\)に対して\((X, Y)\)が一意に定まる(つまり\((x, y)\)に対応する\((X, Y)\)は一つしか存在せず、2つ以上はない)ので、この対応関係は写像ですね。
2.さらに、\((X, Y)\)になるような\((x, y)\)は一つしか存在せず、2つ以上はないので単射ですね。
3.そして、(とりあえず実数の範囲で)任意の\((X, Y)\)に対して、対応する\((x, y)\)が存在するので全射ですね。
以上から全単射の写像であることがわかります。