【ガチャの確率】狙ったSSRが出るまで引く回数の期待値【幾何分布】

以前、「n回引いて排出確率pのSSRが1枚以上出る確率」を計算する記事をかきました。

例えば、100回引いたときに排出確率1%のSSRが1枚以上出る確率は約63.4%でした。

（これは100回連続ではずれる確率\(0.99^{100}\)を1から引いて求めていました）

では狙ったSSRが出るまで引く回数の期待値はどうなっているのか。

これは幾何分布の期待値として求まりますが、

幾何分布を説明するためにまずはベルヌーイ試行を説明します。

その後幾何分布の期待値と分散や二項分布を見ていきます。

ベルヌーイ試行とは次の3つの条件を満たすような試行のことです。

例えばコイントスは、前回の試行などが次の試行に影響したりせず、裏か表の2値で、どちらも確率は\(\frac{1}{2}\)で一定なのでベルヌーイ試行です（コインが立ったりしなければ）。

幾何分布

各試行の成功確率が\(p\)のベルヌーイ試行を成功するまで繰り返すとき、初めて成功するのが何回目かは幾何分布に従います。

（※成功するまでの失敗した回数を確率変数とする定義もあります）

例えば、ガチャを出るまで引くときに\(X\)回目に出たとすると、\(X\)は幾何分布に従い、確率関数は

\[f(x) = p(1 – p)^{x-1}\]

となります。これは\(x-1\)回連続で失敗した後に\(x\)回目で初めて1回成功したことからすぐにわかります。

この幾何分布に従う確率変数は「成功するまでの試行回数」なので、これの期待値を考えればだいたい何回くらいで成功するのかを考えることができます。

導出はしませんが、幾何分布の期待値と分散はそれぞれ

\begin{align*}
E[X] &= \frac{1}{p} \\
V[X] &= \frac{1 – p}{p^2}
\end{align*}

となります。

つまり、確率1%で出るガチャを出るまで引くとしたら平均的に100回くらい引くことになるだろうという予想ができます。ちなみに標準偏差を計算すると99です。

前回の記事のグラフはこの幾何分布の累積分布関数でした。

\(p = 0.01\)の幾何分布の累積分布関数の\(n=400\)までをグラフにすると次のようになります。

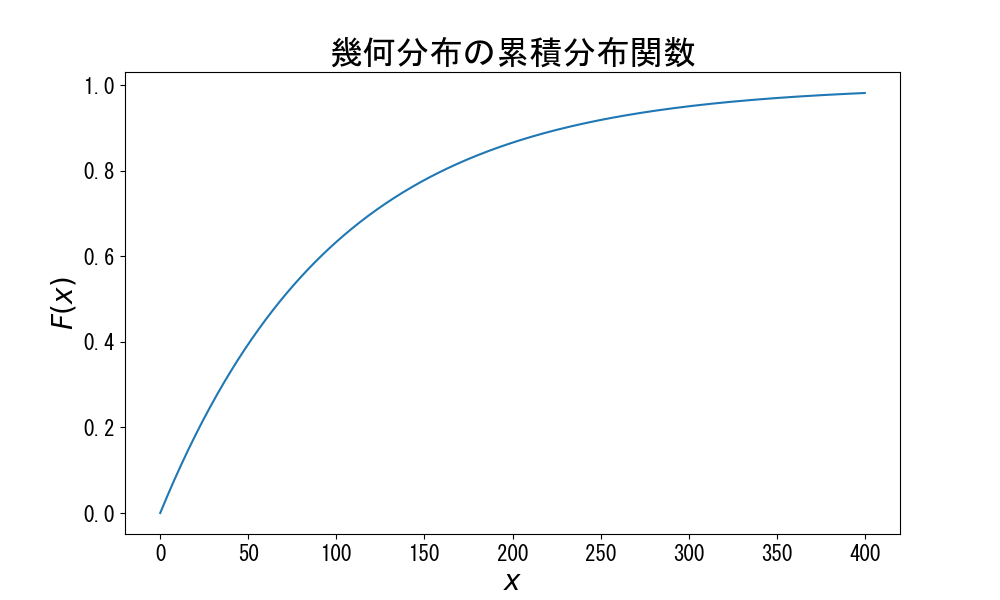
幾何分布は毎回が独立な試行を考える確率分布でしたが、独立でないもので同じようなことを考える確率分布には超幾何分布があります。

ベルヌーイ試行を\(n\)回やったときに、成功回数\(X\)が従う確率分布が二項分布です。

二項分布の形は全体の試行回数\(n\)と成功確率\(p\)によって決まり、確率変数\(X\)がこのような二項分布に従うことを\(X～B(n, p)\)と書きます。

\[f(x) = {}_n \mathrm{ C }_x p^x (1 – p)^{n – x}\]

例えばガチャを100回引いて排出確率1%のキャラが何枚でるかは次のような分布になります。

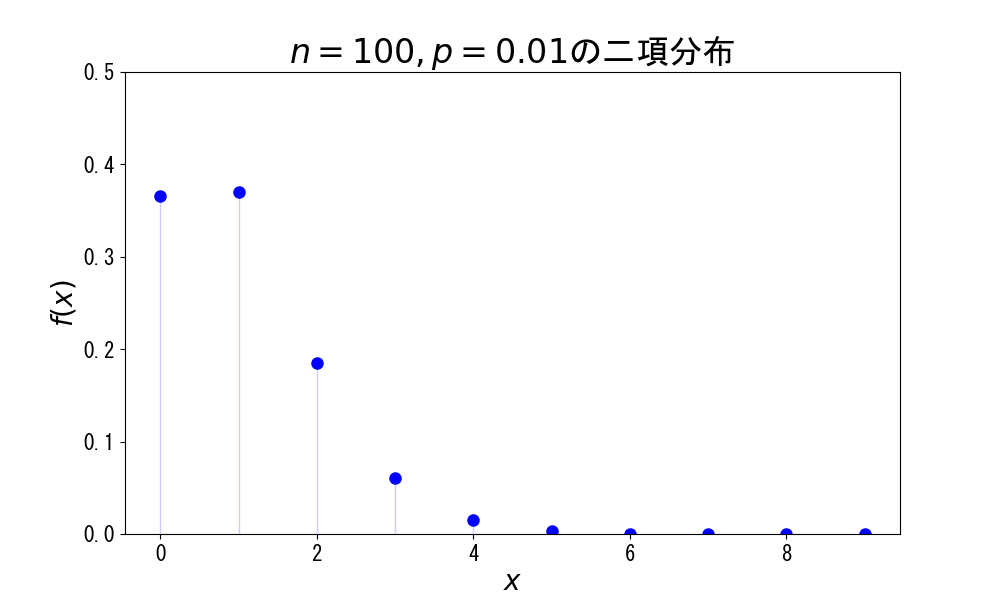
これは、0枚出る確率が37%くらい、1枚出る確率が38%くらい、2枚出る確率が19%くらいというようなことを表しています。

前回の記事では、この分布の1枚以上出る部分の確率を足し合わせたものを、0枚出る確率を1から引いて計算していました。

図の作成はこちらの記事を参考にさせていただきました。

ちなみに\(n\)が大きくて\(p\)が小さいときにはポアソン分布で近似できたり、分散\(np(1-p)\)が十分に大きいときは正規分布で近似できるらしいです。