まず最初に、複素関数の線積分の重要な性質を確認しておきましょう。
複素関数の線積分の注意点
被積分関数が\(f(z)\)の線積分\(\int_C f(z) dz\)の値は
- \(f(z)\)が正則のとき、始点と終点のみで積分の値が決定する(\(f(z)\)によらない)。
- \(f(z)\)が正則でないときは、始点と終点が同じでも\(f(z)\)によって異なる値をとる。
コーシーの積分定理
複素関数\(f(x)\)が単純閉曲線\(C\)とその内部の領域\(D\)で正則であるとき
\[\oint_C f(z) dz = 0\]
が成り立ちます。
\(f(z)\)が正則で、1周しているから始点と終点も同じなので、原始関数の引き算を考えたらたしかに0になりそうですね。
証明は、グリーンの定理で左辺を変形して、そこにコーシー・リーマンの方程式をつかえばできます。
また、\(C\)上に始点と終点として点\(\alphaと\beta\)をおいてみると、積分路を\(c_1とc_2\)とわけることができます。\(c_1とc_2\)の積分路を合わせて周回積分という形になるので、そこにコーシーの積分定理を用いれば先の「始点と終点のみで積分の値が決定する」という性質が示せます。
コーシーの積分定理の応用(多重連結領域へ)
先の考えていた領域\(D\)は中が全部正則でしたが、実は多重連結領域へも応用がききます。
領域\(D\)にひとつぽっかりと穴をあけてくり抜いたような領域を2重連結領域といい、ぽっかりと穴が2つあいていると3重連結領域というらしいです。
(とてつもなく汚い図ですいません…)

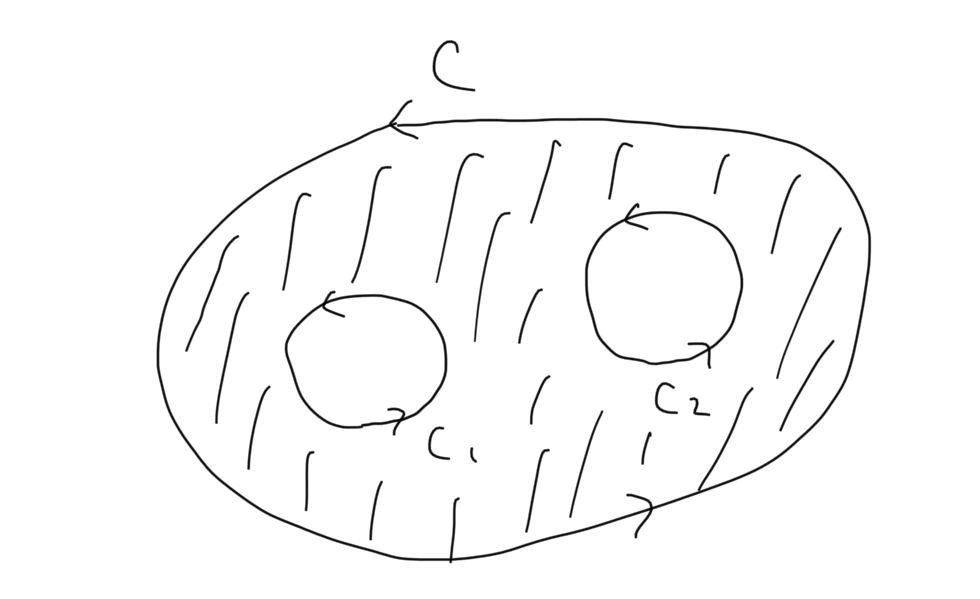
切り込みを入れても、真っ二つにぶった切ってもいいですが、とにかく図を書けばコーシーの積分定理から多重連結領域では次のように計算できることがわかります。
左図では、\[\oint_C f(z) dz = \oint_{C_1} f(z) dz\]
右図では、\[\oint_C f(z) dz = \oint_{C_1} f(z) dz + \oint_{C_2} f(z) dz\]
これ以上の多重連結領域でも同様に計算できます。
周回積分公式
積分路が\(C:| z – \alpha | = r (r > 0 , ~\alpha \in \mathbb{C})\)で、\(f(z) = (z – \alpha) ^ n\)に対して、
\begin{eqnarray}
\oint_{C_0} (z – \alpha) ^ n dz
=
\begin{cases}
2 \pi i & (n = -1) \\
0 & (n \neq -1)
\end{cases}
\end{eqnarray}
ということが、計算してみるとわかります。
そして、これにコーシーの積分定理を用いれば、
\(\alpha\)を囲む一般の単純閉曲線\(C\)を積分路としても、
\[\oint_{C} \frac{1}{z~ – \alpha} ~dz = 2 \pi i\]
となります。これは周回積分公式と呼ばれ、これによって留数定理で簡単に積分が計算できるようになります。
コーシーの積分公式(グルサの定理もいっしょに)
先の多重連結領域への応用と周回積分公式によって、特異点を含む領域では、特異点ごとに計算すればよいことがわかりました。
そんなときに、この公式が役に立ちます。
\[\oint_C \frac{f(z)}{(z – \alpha)^{n+1}} dz = \frac{2 \pi i}{n!} f^{(n)}(\alpha)\]
\(n=0\)のときがコーシーの積分公式の形になります。
\(f(\alpha)\)が左辺にくる書き方がよくあるように、コーシーの積分公式は\(f(\alpha)\)の表現の1つとみることもできます。
留数定理
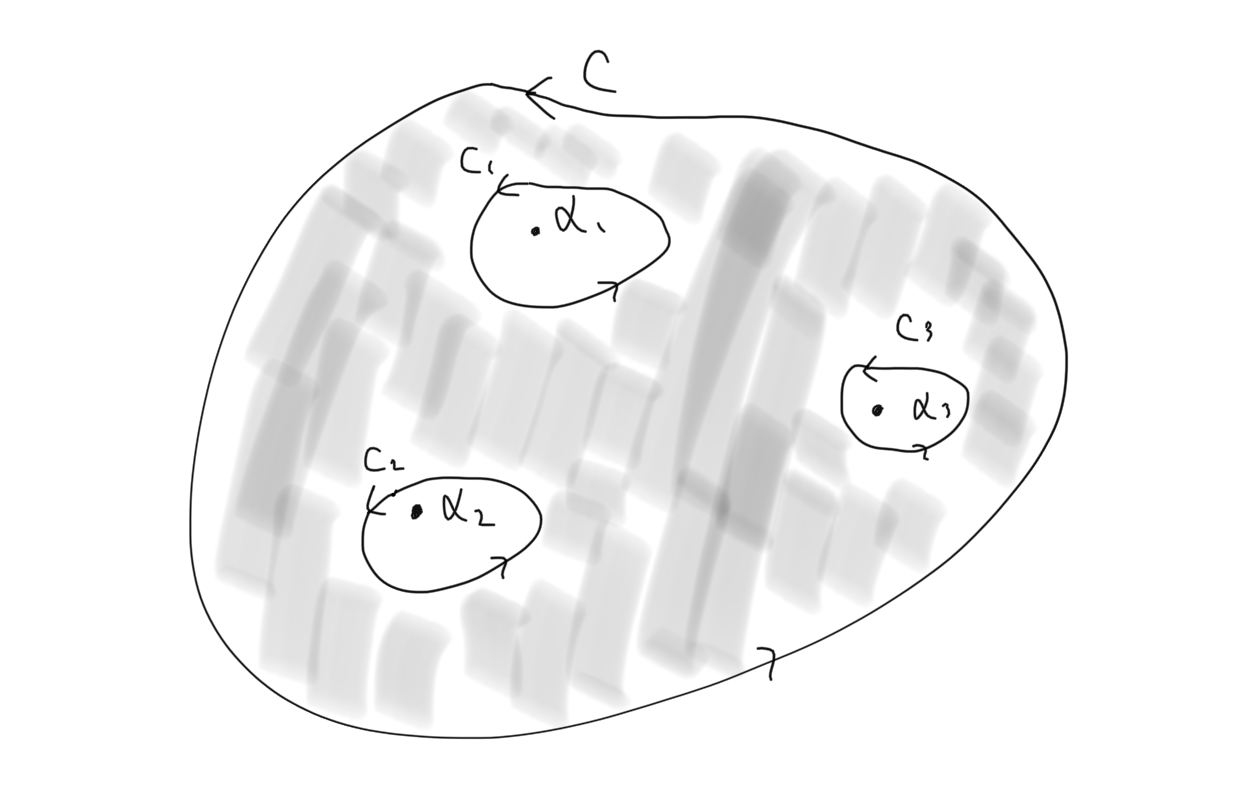
留数定理は、先の周回積分公式とローラン展開とコーシーの積分定理の応用をくっつけたようなやつです。
ローラン展開をしたときの\( – 1\)乗になっている項の係数を留数と呼ぶと、項別積分を考えれば留数以外の項は積分のとき0になることが先の周回積分からわかります。
そこでコーシーの積分定理の応用のように、単純閉曲線\(C\)の内部にある孤立特異点ごとに留数を計算して、それを足し合わせて\(2 \pi i\)かけてやれば、積分路\(C\)の積分が計算できることになります。
図では、次のように計算できます。
便利ですね。
留数は次のように計算できます。
\(f(z)\)の位数kの極 \(\alpha\) の留数は
\[Res( \alpha ) =\displaystyle \frac{1}{(k – 1)!} \lim_{z \to \alpha} {\frac{d^{k-1}}{dz^{k-1}} (z – \alpha )^k f(z) } \]
コーシーの積分公式やその応用のグルサの定理などの計算とあまり違いがないように感じた人もいると思うのですが、中身は同じようなものだと思います。
おそらく、留数定理は積分の値を求めるための計算方法で、コーシーの積分公式は\(f(\alpha)\)の表現を与えるという見方ができる違いがくらいかなと思います。
もっとちゃんと書いてある本が欲しい人、証明も欲しい人、計算や演習もしたい人は、おすすめの複素解析の本があるのでぜひ見てみてください。


