直交射影行列と斜交射影行列の計算
\(\text{Span}(A)\)への直交射影行列Pは
\[P = A({}^t \! A A)^{-1} {}^t \! A\]
で計算できます。
また、\((\text{Span}(B))^{\bot}\)に沿った\(\text{Span}(A)\)への斜交射影行列Pは
\[P = A({}^t \! B A)^{-1} {}^t \! B\]
で計算できます。
ただし、\((\text{Span}(B))^{\bot}\)は\(\text{Span}(B)\)の直交補空間で、つまり\(\text{Span}(B)\)のあらゆる元に直交する部分空間です。
2次元空間での計算例
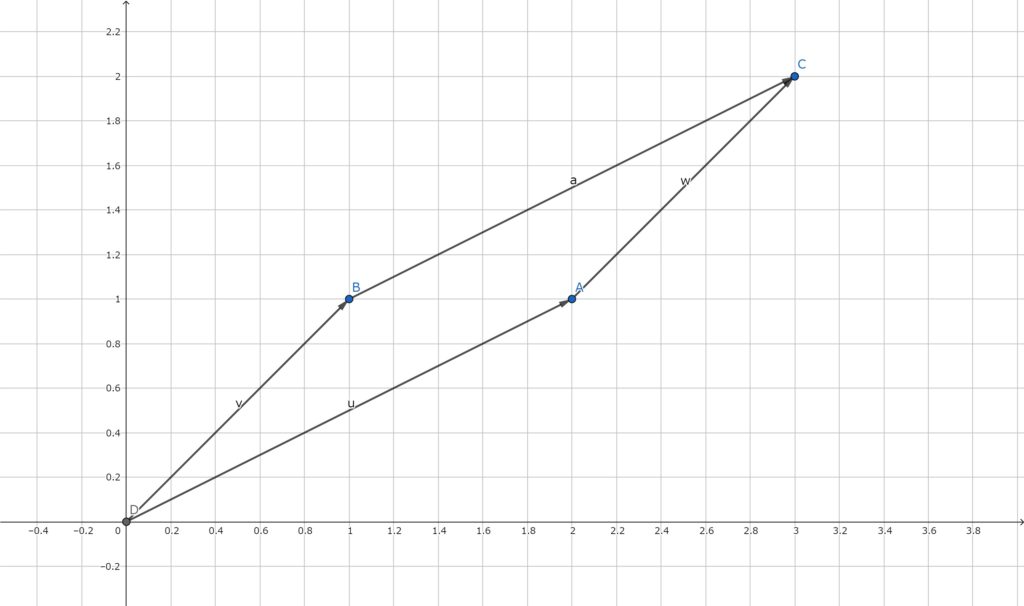
例えば\(A = \left(\begin{array}{c} 2 \\ 1 \end{array}\right)\)と\(B = \left(\begin{array}{c} 1 \\ 1 \end{array}\right)\)について、
\[ \text{Span}(A) \oplus \text{Span}(B) = \mathbb{R}^2 \]
です。これに対し\(\text{Span}(B)\)に沿った\(\text{Span}(A)\)への斜交射影行列\(P_{A}\)は、先のように直交補空間を考えることで計算できます。
Bとの内積を考えると\(\left(\begin{array}{c} -1 \\ 1 \end{array}\right)\)が直交するから
\begin{eqnarray*}
P_{A} &=& \left(\begin{array}{c} 2 \\ 1 \end{array}\right) \left( ~(-1 ~~~1) \left(\begin{array}{c} 2 \\ 1 \end{array}\right) ~\right)^{-1} (-1 ~~~1) \\
&=& \begin{pmatrix} 2 & -2 \\ 1 & -1 \end{pmatrix}
\end{eqnarray*}
これが\(\text{Span}(B)\)に沿った\(\text{Span}(A)\)への斜交射影行列になっているか確かめるために、
\[ A + B = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) + \left(\begin{array}{c} 1 \\ 1 \end{array}\right) = \left(\begin{array}{c} 3 \\ 2 \end{array}\right) \]
を射影してみると
\[ P_{A} \left(\begin{array}{c} 3 \\ 2 \end{array}\right) = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) \]
となり、求めていたものになっていることが計算で確かめられました。
一方で\(\text{Span}(A)\)に沿った\(\text{Span}(B)\)への斜交射影行列\(P_{B}\)は
\[P_{B} = E_2 ~- P_{A} = \begin{pmatrix} -1 & 2 \\ -1 & 2 \end{pmatrix}\]
となります。実際に、
\[ P_{A} \left(\begin{array}{c} 3 \\ 2 \end{array}\right) = \left(\begin{array}{c} 1 \\ 1 \end{array}\right) \]
となり、求めていたものになっていることがわかります。
3次元以上でも同様に計算することができます。
検算にもつかえる意識すべき性質
線形空間Vのk個の部分空間\(W_1, \ldots , W_k\)は、
\[V = W_1 \oplus W_2 \oplus \cdots \oplus W_k\]
を満たし、\(C_i = T_1 + \cdots + T_{i-1} + T_{i+1} + \cdots + T_k\)(つまり\(iに対してT_i\)を抜いた和空間)とします。
このとき、\(C_i\)に沿った\(W_i\)への斜交射影行列を\(T_i\)とすると次の3つの性質を満たします。
・\(T_1 + T_2 + \cdots + T_k = E\)
・\(T_i ^2 = T_i\)(射影の性質)
・\(T_i T_j = O\)(異なるi, j)
※\( {}^t \! ~T = T\)は直交の性質なので注意しましょう。


